离散数学（下）笔记

离散数学（下）

离散数学及其应用 第9章 关系

9.1 关系及其性质

• 一个从$A$到$B$的关系$R$定义为一个$A\times B$的子集。
  • 一个在$A$上的关系$R$就是一个$A\times A$的子集。
• 自反性（reflexive）：对于任意的$a\in A$均有$(a,a)\in R$。
• 对称性（symmetric）：对于任意的$(a,b)\in R$均有$(b,a)\in R$。即关系矩阵中的每一个元素都必有它的对称元素。
  • 反对称性（antisymmetric）：对于任意的$(a,b)\in R$且$(b,a)\in R$，都有$a=b$。即关系矩阵中每一个元素都必没有它的对称元素。
  • 所以对于某些关系来讲，它有一部分元素有他的对称元素，有一部分元素没有它的对称元素，他就既不符合对称性也不符合反对称性。
• 传递性（transitive）：对于任意的$(a,b)\in R$且$(b,c)\in R$，都有$(a,c)\in R$。
• 关系的复合（combination）：设$R$为一个从集合$A$到集合$B$的关系，$S$为一个从集合$B$到集合$C$的关系。则$S$和$R$关系的复合$S\circ R$是一个从集合$A$到集合$C$的关系，其中的每一个元素$(a,c)$中的$a$来自于集合$A$，$c$来自于集合$C$，且存在一个在集合$B$中的元素$b$使得$(a,b)\in R$且$(b,c)\in S$。
  • 先$R$后$S$
• 关系的幂：$R^1=R$，$R^{n+1}=R^n\circ R$
  • 右乘
  • 并不是右乘，只是用复合符号（$\circ$）时把$R$写在$R^n$的右边，代表先算$R$再算$R^n$，但实际上在进行关系矩阵的布尔积时，是左乘。即$M_{R^{n+1}}=M_R\odot M_{R^n}$
• 定理1：一个在集合$A$上的关系$R$具有传递性的充分必要条件是对于任意的$n=1,2,3,\cdots$，都有$R^n \subseteq R$。

9.2 $n$元关系

• 主键（primary key）：若没有两个在关系中的$n$元组在某一个域中有同样的值，那么这个域就被称为主键。
• 复合键（composite key）：某若干域的组合若可以单一的确定一个在$n$元关系中的$n$元组，则这些域的笛卡尔积被称为复合键。

9.3 表示关系

• 关系矩阵
  • $M_{S\circ R} = M_R⊙M_S$
  • $M_{R^n} = M_R^{[n]}$
  • 先算的在左边，和关系的复合表示相反
• 有向图
  

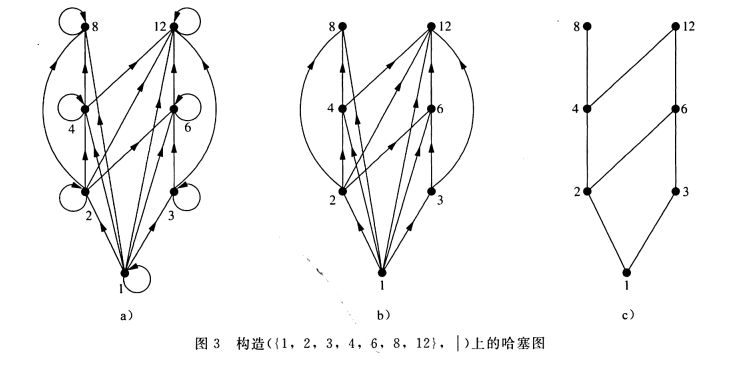
9.4 关系闭包

• 关系闭包（Closures of Relations）：设$R$是一个在集合$A$上的关系，则$R$关于性质$P$的关系闭包$S$是这样一种关系：它具有性质$P$且包含关系$R$，同时被$A\times A$中的所有具有性质$P$的关系包含着。
• $R$的传递关系闭包$R^*$的关系矩阵是
  $$
  M_{R^*}=M_R\lor M_R^{[2]}\lor\cdots\lor M_R^{[n]}
  $$
  寻找自反关系闭包和对称关系闭包都很简单，关键在于寻找传递关系闭包。
• 算法1：
  
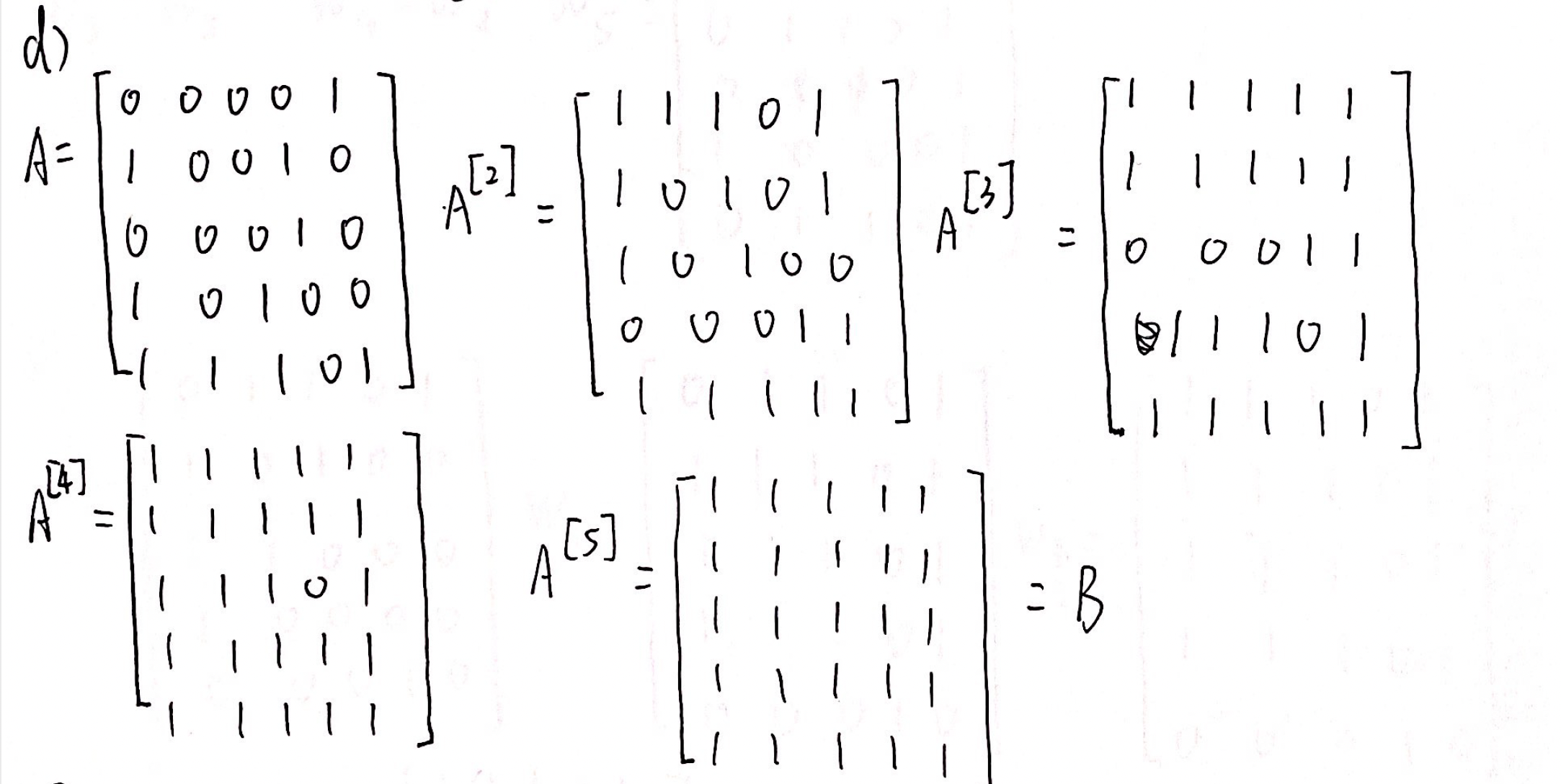
• Warshall算法
  在构造$W_k$的时候，先看第$k$列哪几行是1，那么这些行就必须要包含第$k$行所包含对应位置上所有的1（同时也要包含自己本来就有的1）。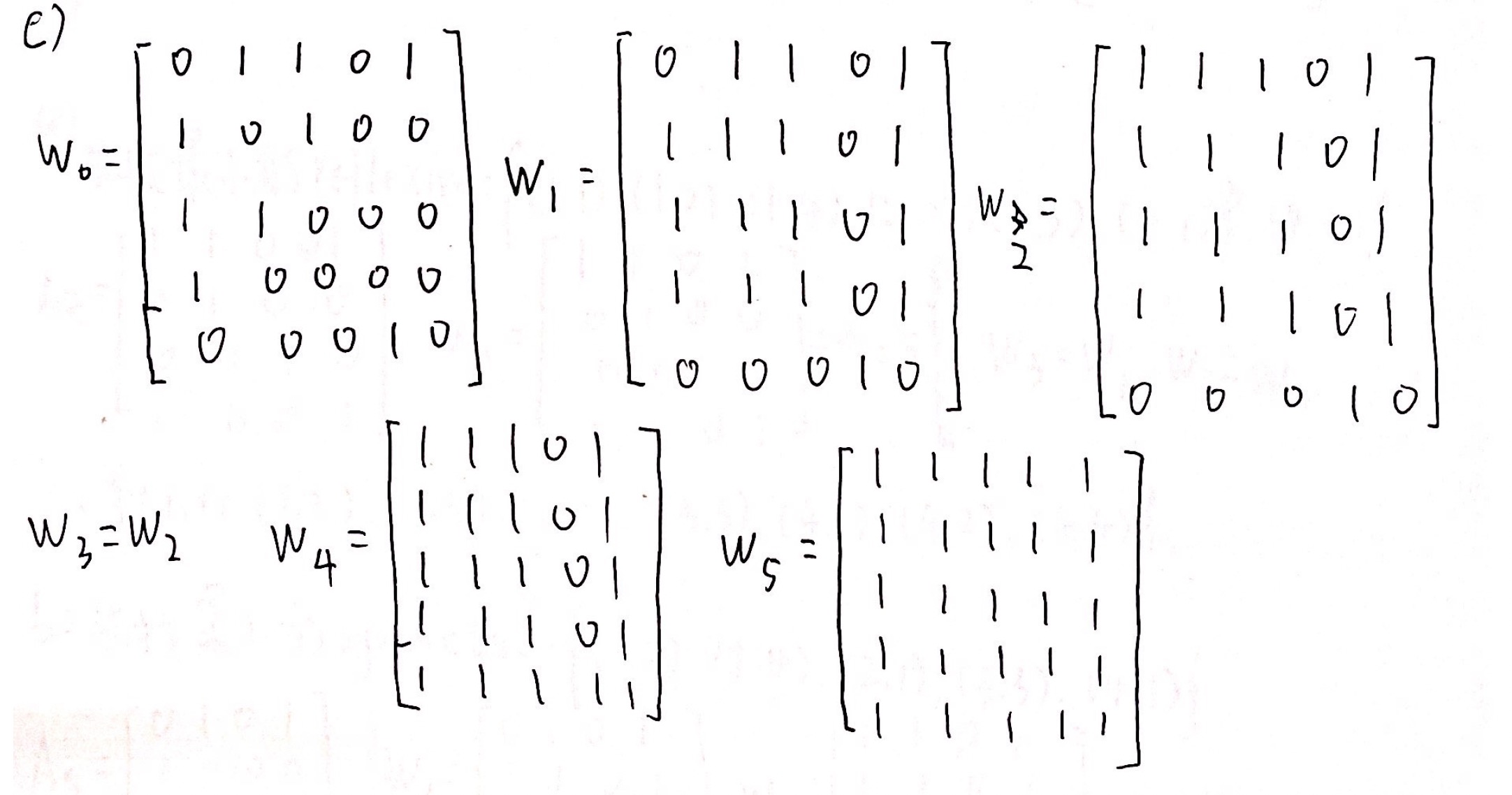
  

9.5 等价关系

• 等价关系（equivalence relation）：若一个定义在集合$A$上的关系是自反的，对称的和传递的，那么这个关系就被称为等价关系。
  
• 等价类（equivalence classes）：若$R$是一个定义在集合$A$上的关系，那么所有和$A$中元素$a$满足关系$R$的元素的集合被称为$a$的等价类。用$[a]_R$表示，若语境下只有一个关系，可以简写为$[a]$。
• 每一个等价关系都对应着一组等价类，这些等价关系的等价类们都可以构成集合$A$的一个划分。

9.6 偏序关系

• 偏序关系（partial ordering）：若一个定义在集合$A$上的关系是自反的，反对称的和传递的，那么这个关系就被称为偏序关系。$A$中的元素被称为偏序集的元素。
• 若偏序集$(S,\preceq)$中的两个元素$a$和$b$满足$a\preceq b$或$b\preceq a$则称这两个元素是可比的，否则则称为不可比的。
• 若偏序集$(S,\preceq)$中的任意两个元素$a$和$b$都是可比的，则称$S$是一个线序集，$\preceq$是一个线序关系。
• 若偏序集$(S,\preceq)$是一个线序集，且每一个$S$的非空子集中都有一个最小（least）的元素则称$(S,\preceq)$是一个良序集。
• 哈赛图（Hasse Diagrams）：有向图省略了箭头，自反关系的圆圈，和可以由传递关系决定的关系。
• 极大（maximal）元和极小（minimal）元：
  • 对于一个偏序集中的元素$a$来说，若不存在一个元素$b$使得$a\prec b$，则称$a$是这个偏序集中的一个极大元。
  • 对于一个偏序集中的元素$a$来说，若不存在一个元素$b$使得$b\prec a$，则称$a$是这个偏序集中的一个极小元。
  • 在一个偏序集中可以同时存在多个极大元和极小元
• 最大（greatest）元和最小（least）元
  • 对于一个偏序集中的元素$a$来说，若对于任意一个元素$b$都可以使得$b\preceq a$，则称$a$是这个偏序集中的一个最大元。
  • 对于一个偏序集中的元素$a$来说，若对于任意一个元素$b$都可以使得$a\preceq b$，则称$a$是这个偏序集中的一个最小元。
  • 如果存在的话，一个偏序集中最多只有一个最大元和一个最小元。
• 上界（upper bound）和下界（lower bound）
  • 设$A$是一个偏序集$(S,\preceq)$的子集，若对于偏序集$S$中的一个元素$u$来说，任意一个$a\in A$都有$a\preceq u$，则称$u$是集合$A$的一个上界。
  • 设$A$是一个偏序集$(S,\preceq)$的子集，若对于偏序集$S$中的一个元素$u$来说，任意一个$a\in A$都有$u\preceq a$，则称$u$是集合$A$的一个下界。
  • 最小上界（LUB）和最大下界（GLB）
    • 集合$A$中所有上界中，最小的上界被称为最小上界。
    • 集合$A$中所有下界中，最大的下界被称为最大下界。
• 格（lattice）：若在一个偏序集中，对于任意两个元素，都可以找到它们的最小上界和最大下界，则称这个偏序集为一个格。

离散数学结构 第9章 半群与群

9.1 二元运算

• 二元运算：集合$A$上的二元运算是一个处处有定义的函数$f:A\times A\rightarrow A$。它必须满足以下性质：
  1. $Dom(f) = A\times A$，即二元运算必须为$A$的每个有序元素对而定义。
  2. 因为二元运算是一个函数，所以每个有序对仅对应$A$中唯一的元素。

     可以定义在有$n$个元素的集合上的二元运算共有$n^{n^2}$个。

• 二元运算的性质
  1. 交换性（commutative）：如果对于$A$中的所有元素有$a\ast b=b\ast a$，则称集合$A$上的二元运算是交换的。
  2. 结合性（associative）：若对于$A$中任意的$a,b,c$都有$a\ast(b\ast c)=(a\ast b)\ast c$，则称$A$上的二元运算是结合的。
  3. 幂等性（Idempotent）:若对于$A$中任意的$a$都有$a\ast a=a$，则称$A$上的运算是幂等的。

9.2 半群

将一个集合$S$和一种运算$\ast$组合起来成为$(S, \ast)$，根据$\ast$的性质不同，可以得到以下几种不同的数学结构：

1. 广义群（groupoid）：封闭性；
2. 半群（semigroup）：封闭性，结合性；
   • 单位元（identity）：在半群$(S,\ast)$中若存在这样一个元素$e$，对于所有的$a\in S$都有$e\ast a=a\ast e=a$，那么就称它为单位元。
3. 幺半群（monoid）：封闭性，结合性，具有单位元；
4. 在以上结构的基础上，若对应的运算还满足交换性，则被称为”交换xxx“。如满足交换性的半群被称为”交换半群“。

• 自由半群（free semigroup）：从半群$(A,\cdot)$中自由地选取任意多的元素，以任意的次序进行运算，得到的所有结果的集合被称为自由半群，用$(A^\ast,\cdot)$表示。

  默认$\cdot$运算为字符串的拼接

• 定理：如果$a_1,a_2,\cdots,a_n(n\geq 3)$是半群中的任意元素，那么在由元素$a_1,a_2,\cdots,a_n$形成的积中任意插入有意义的括号，积的结果都是相等的。
• 子半群（subsemigroup）和子幺半群（submonoid）：
  • 设$(S,\ast)$是一个半群，$T$是$S$的一个子集，如果$T$在运算$\ast$下是封闭的，那么称$(T,\ast)$是$(S,\ast)$的子半群。
  • 在$(S,\ast)$是幺半群的情况下，那么在上一条的基础上再加上$e\in T$，则称$(T,\ast)$是$(S,\ast)$的子幺半群。
• 同构（isomorphism）和同态（Homomorphism）:
  • 设$(S,\ast)$和$(T,\ast ')$是两个半群，如果有一个处处有定义的函数$f:S\rightarrow T$对于$S$中所有的$a$和$b$有$f(a\ast b)=f(a)\ast 'f(b)$，则称$f$是从$(S,\ast)$到$(T,\ast ')$的一个同态。
  • 在此基础上，如果$f$还是一个满射，则称$T$是$S$的同态像。
  • 在此基础上，如果$f$还是一个双射，则称$f$是从$(S,\ast)$到$(T,\ast ')$的一个同构。

9.3 半群的积与商

本节介绍了两种从已有半群得到新半群的方法

1. 通过做积：若$(S,\ast)$和$(T,\ast')$是两个半群，则$(S\times T,\ast'')$是一个半群。其中$\ast''$是被等式$(s_1,t_1)\ast''=(s_1\ast s_2,t_1\ast' t_2)$所定义的。
   在介绍第二种方法前，需要先知道什么叫做同余关系。

• 同余关系（congruence relation）：一个在群$(S,\ast)$上定义的等价关系$R$，如果可以由$aRa'$和$bRb'$推出$(a\ast b)R(a'\ast b')$，则称$R$为一个同余关系。

  证明同余关系的步骤：
  1. 先证明它是一个等价关系；
  2. 再证明可以由$aRa'$和$bRb'$推出$(a\ast b)R(a'\ast b')$。

• 可以从等价关系和集合划分的对应关系上，定义$[a]$是包含$a$的等价类，$S/R$表示所有等价类的集合。

2. 通过做商：若$(S,\ast)$是一个半群，$R$是定义在这个半群上的一个同余关系。则$(S/R, \circledast)$是一个半群。其中$\circledast$是被等式$[a]\circledast [b]=[a\ast b]$所定义的。称$S/R$为商半群。

• 推论：幺半群的商半群依然是幺半群。

• 定理：若$(S,\ast)$是一个半群，$(S/R, \circledast)$是对应的商半群，那么由$f_R(a)=[a]$定义的函数$f_R:S\rightarrow S/R$是一个同态，且是满射，称其为自然同态。

• 定理：设$f:S\rightarrow T$是半群$(S,\ast)$到半群$(T,\ast')$的一个同态像，$R$是$S$上的关系且定义为对于$S$中的$a$和$b$，$a R b$当且仅当$f(a)=f(b)$。那么

  1. $R$是一个同余关系。
  2. $(T,\ast')$和商半群$(S/R, \circledast)$是同构的。

  此处经菌神确认，书上所写的”同态“并不准确，应为”同态像“。

9.4 群

• 群（group）：封闭性，结合性，具有单位元，每个元素都有它的逆元。
• 定理：设$G$是一个群，则$G$中的每个元素$a$在$G$中有且仅有一个逆元。
• 设$G$是一个群，则对于群中的元素$a,b,c$有以下性质
  1. $ab=ac\Rightarrow b=c$；
  2. $ba=ca\Rightarrow b=c$；
  3. 对于一个函数$M_a:G\rightarrow G$满足$M_a(g)=ag$，则$M_a$是单射；
  4. $(a^{-1})^{-1}=a$；
  5. $(ab)^{-1}=b^{-1}a^{-1}$；
  6. 方程$ax=b$在$G$中有唯一解；
  7. 方程$ya=b$在$G$中有唯一解。
• 如果$G$是具有有限元素的一个群，则称$G$是有限群，$G$的阶是$G$中的元素个数$|G|$。
• 对于固定的元素标号来说1阶，2阶，3阶的群只有一个，4阶的只有两个。

  $Z_2\times Z_2$和$Z_4$都是4阶群，但$Z_2\times Z_2$是克莱因群，$Z_4$不是克莱因群。但4阶不同形态的群只有两个，所以所有的四阶群要么和$Z_2\times Z_2$同构，要么和$Z_4$同构。
  克莱因群：克莱因群是最小的四阶非循环群

• 群的重要例子：三角对称群
  
  
• 群的重要子集：子群
  设$H$是群$G$的一个子集，使得：
  1. $G$的单位元$e$属于$H$；
  2. 如果$a$和$b$属于$H$那么$ab\in H$；
  3. 如果$a\in H$那么$a^{-1}\in H$。
     则称$H$是$G$的一个子群。

     如何寻找子群：
     1. 先将单位元加入到集合中；
     2. 加入一个元素，同时加入它的逆元和它本身的任意次幂；
     3. 再加入第上一步加入的所有元素的逆元和它们的任意次幂，直到无需加入更多元素。

• 设$G$是一个群，则$G$和$H={e}$是$G$的子群，称它们为$G$的平凡子群。
• 定理：设$(G,\ast)$和$(G',\ast')$是两个群，$f:G\rightarrow G'$是从$G$到$G'$的一个同态。
  1. 如果$e$是$G$的单位元，$e'$是$G'$的单位元，则$f(e)=e'$;
  2. 如果$a\in G$，则$f(a^{-1})=(f(a))^{-1}$
  3. 如果$H$是$G$的一个子群，那么
     $$
     f(H)=\{f(h)|h\in H\}
     $$
     是$G'$的一个子群。

9.5 群的积与商

以下两种通过积和商的途径得到新群的方式与半群类似。

1. 通过做积：若$G_1$和$G_2$是群，那么$G=G_1\times G_2$是二元运算由$(a_1,b_1)(a_2,b_2)=(a_1a_2,b_1b_2)$定义的群。
2. 通过做商：设$R$是群$(G,\ast)$上的一个同余关系，那么半群$(G/R, \circledast)$是一个群，其中运算$\circledast$在$G/R$上且满足$[a]\circledast [b]=[a\ast b]$。

• 推论
  • 如果$R$是$G$上的一个同余关系，那么由$f_R(a)=[a]$给出的函数$f_R:G\rightarrow G/R$是群的同态。
  • 如果$f:G\rightarrow G'$$是从群(G,\ast)$到群$(G',\ast')$上的一个同态且是满射，$R$是定义在$G$上的关系，满足$a R b$当且仅当对$G$中的$a$和$b$有$f(a)=f(b)$，那么：
    1. $R$是一个同余关系。
    2. 由$\overline{f}([a])=f(a)$给出的函数$\overline{f}:G/R\rightarrow G'$是从群$(G/R, \circledast)$到群$(G',\ast')$的一个同构且是满射。
• 左/右陪集（left/right coset）和正规（normal）子群：设群$H$是群$G$的一个子群，$a\in G$，由$a$决定的$G$中$H$的左陪集是集合$aH=\{ah|h\in H\}$，右陪集是$Ha=\{ha|h\in H\}$。最后如果对$G$中所有的$a$有$aH=Ha$，则称$G$的子群$H$是正规子群。

  如何寻找正规子群：

  1. 先将单位元加入到集合中；
  2. 加入一个元素，同时加入它的逆元和它本身的任意次幂；
  3. 再加入第上一步加入的所有元素的逆元和它们的任意次幂，直到无需加入更多元素。
     （前三步就是在寻找子群，在此再重述一遍）
  4. 判断找到的这个子群$H$是否满足对于任意的$a\in G$都有$aH=Ha$。

• 警告 如果$Ha=aH$，由此并不能得到：对于$h\in H$和$a\in G$，有$ha=ah$，而只能得到$ha=ah'$，其中$h'$是$H$中的某个元素。
• 若$H$是$G$的一个子群，在计算$H$的所有左/右陪集时，当$a\in H$时不需要计算$aH$或$Ha$，因为$aH=Ha=H$。这一结论在书上384页有非常精彩的证明，在此不再赘述。（🍄神的博客里有相关的证明）
• 定理：设$R$是群$G$上的一个同余关系，$H=[e]$，即包含单位元的等价类，那么$H$是$G$的一个正规子群，并且对每个$a\in G$，$[a]=aH=Ha$。
  由这条定理可以看到在这种情况下商群$G/R$是由$N=[e]$的所有左陪集所构成的，$G/R$中的运算由
  $$
  (aN)(bN)=[a]\circledast [b]=[ab]=abN
  $$
  给出。正因如此，常把$G/R$写成$G/N$。
• 定理：设$N$是群$G$的一个正规子群，$R$是$G$的下述关系：$a R b$当且仅当$a^{-1}b\in N$。那么：
  1. $R$是$G$上的同余关系；
  2. $N$是关于$R$的等价类$[e]$，其中$e$是$G$的单位元。
• 核（kernel）：设$f$是从群$(G,\ast)$到群$(G',\ast')$上的同态并且是满射，$f$的核记作$\ker(f)$，定义为：
  $$
  \ker(f)=\{a\in G|f(a)=e'\}
  $$
  那么

1. $\ker(f)$是$G$的一个正规子群；
2. 商群$G/ker(f)$与$G'$是同构的。

第11章 群与编码

11.1 二元信息码与检错码

• 先定义一个集合$B=\{0,1\}$，那么集合$B$在模二加法的运算下是一个群。
• 那么$B^m=B\times B\times\cdots\times B$（m个因子）在$\oplus$运算（按位异或）下是一个群。他有以下特点：
  • 单位元是$\overline{0}=00\cdots 0$；
  • 每个元素都是自身的逆元；
  • 阶（元素数量）为$2^m$
• 信息传输的基本任务是减小收到的字不同于发送的字的可能性，采用以下方法可以做到这一点。首先选取一个整数$n>m$和单射函数$e:B^m\rightarrow B^n$。函数$e$称为一个$(m,n)$编码函数，并且可以把它看做是$B^m$中的每个字表示成$B^n$中的一个字的一种方法。如果$b\in B^m$，那么$e(b)$称作表示b的代码字。附加的01能够提供一种方法检测或纠正在传输通道中所产生的错误。
• 注意到$e$是单射，所以$B^m$中的每个字将被指定为不同的代码字。
• 设被发送码字$b\in B^m$，代码字$x=e(b)\in B^n$，接收字$x_t\in B^n$
• 一般地，传输中总是会有错误发生。如果$x$和$x_t$中至少有一个但不超过k个位置不同，则称代码字$x=e(b)$有k个或更少的错误传送
• 若每当$x=e(b)$有$k$个或更少的错误被传送时，则$x_t$不是一个代码字，则说$e$检测到k个或更少的错误。
• 对于$x\in B^n$，$x$中1的个数称作$x$的权，并用$|x|$表示。
• 奇偶校验码 若$|b|$为偶数，则在最后补0；若$|b|$为奇数，则在最后补1。如此便形成了一个编码函数$e:B^m\rightarrow B^{m+1}$，最后一位称为奇偶校验码。很明显，这种编码只能检测到1个错误，对于所有的$|x_t|$为偶数的情况无能为力，不过尽管如此，奇偶校验码还是被广泛的使用。
• Hamming距离 $x$与$y$之间的Hamming距离$\delta(x,y)=|x\oplus y|$，使用Hamming距离计算两个二进制串$x$和$y$之间不同位的个数非常方便。
• Hamming距离的性质
  • $\delta(x,y)\leq\delta(x,z)+\delta(z,y)$
    Hamming距离的性质当然不止这一条，只不过别的都是显然的，在此只说这一条
• 定理：一个$(m,n)$编码函数$e:B^m\rightarrow B^n$能够检测$k$个或更少错误当且仅当它的最短距离至少是$k+1$。
  • 一般的来说，要计算这个最短距离，需要把所有的$B^n$都列出来，然后两两计算距离，找出最短距离。最差情况要做$C_{2^m}^2$次计算，非常折磨。

---

但

• 确实意识到，本章到了目前为止都还没有用到一个非常好的东西，就是$(B^n,\oplus)$是一个群这一事实。下面将考虑利用$B^n$的这个性质的编码函数。
• 群码 一个$(m,n)$编码函数$e:B^m\rightarrow B^n$称为一个群码，若
  $$
  e(B^m)=\{e(b)|b\in B^m\}={\rm Ran}(e)
  $$
  是$B^n$的一个子群。

  如何检验一个编码函数（N）是否是群码

  1. $00\cdots 0$在$N$中
  2. 若$x$和$y$属于$N$，则$x\oplus y\in N$。
     定理：设$e:B^m\rightarrow B^n$是一个群码，那么$e$的最短距离是非0代码字的最小权。

• 根据这条定理可以发现，算群码的最短距离是非常简单的，只需要把所有非0码字的权算出来就可以了。但确定一个编码是不是群码却要费和之前基本等同的功夫（计算步骤2需要$C_{2^m}^2$次计算）。所以我们就在想：可不可以构造一套方法，使我们只要按照这种固定的方法得到的编码就一定是群码，从而省去检查一个编码是否是群码的过程。为了介绍这种方法，我们需要先定义两种布尔矩阵的运算。

1. 设$D=[d_{ij}]$，$E=[e_{ij}]$，则由$D\oplus E=F$定义的$F=[f_{ij}]$有$f_{ij}=d_{ij}\oplus e_{ij}$。
   • 对应位置取异或
2. 设$D=[d_{ij}]$是一个$m\times n$布尔矩阵，$E=[e_{ij}]$是一个$n\times p$布尔矩阵，则由$D*E=F$定义的$F=[f_{ij}]$有
   $$
   f_{ij}=d_{i1}e_{1j}+d_{i2}e_{2j}+\cdots +d_{ip}e_{pj}
   $$
   • 相应行列有多少个1在相同位置，若为奇数个则为1，偶数个则为0
   • 注意：与矩阵的布尔积（$\odot$）相区分
     定理：
     $$
     (D\oplus E)*F=D*F\oplus E*F
     $$
     现在把元素$x=x_1x_2\cdots x_n$看成是$1\times n$矩阵。
     定理：设$m$和$n$是非负整数且$m<n,r=n-m,H$是一个$n\times r$布尔矩阵，那么函数$f_H:B^n\rightarrow B^r$定义为
     $$
     f_H(x)=x*H
     $$

是群$B^n$到$B^r$的一个同态。

• 推论：在这种情况下
  $$
  N=\{x\in B^n|x*H=\overline{0}\}
  $$
  是$B^n$的一个正规子群。原因可见9.5末尾。

下面开始考虑这样一个布尔矩阵

这是一个$n\times r$布尔矩阵，它的最后$r$行形成了一个$r\times r$单位矩阵，称$H$为奇偶校验矩阵。
下面用$H$定义一个编码函数$e_H:B^m\rightarrow B^n$，若$b=b_1b_2\cdots b_m$，那么设$x=e_H(b)=b_1b_2\cdots b_mx_1x_2\cdots x_r$，其中$x_1x_2\cdots x_r$就是$b$和$H$的前$m$行做$*$运算得到的。
定理：设$x=y_1y_2\cdots y_mx_1x_2\cdots x_r\in B^n$，那么$x*H=\overline{0}$仅对某个$b\in B^m,x=e_H(b)$。

• 推论：$e_H(B^m)=\{e_H(b)|b\in B^m\}$是$B^n$的一个子群。
  至此，我们终于得到了一种可以稳定构造群码的方法，即：构造一个奇偶校验矩阵，用$B^m$中的每一个元素乘以它的前m行，得到的$B^r$拼接在他的后面，便是一套群码。并且通过这样的方法得到的$B^n* H$一定等于$\overline{0}$。

11.2 译码与纠错

在上一节，我们很好的利用群码已经解决了作为发送方该如何编码的问题，本节解决接收方如何译码的问题。

译码函数：一个满射函数$d:B^n\rightarrow B^m$称作是与$e$有关的译码函数，若$d(x_t)=b’\in B^m$使得当传输通道没有任何噪声时，$b’=b$。

• 注意到课本原文强调$d$是一个满射函数，而同时没有讲他不是一个单射函数。事实上$d$必不是一个单射函数，他的定义域需要覆盖$B^n$中所有的元素，因为一定有许多不同的$B^n$对应同一个$B^m$。
  设$e$是一个$(m,n)$编码函数，$d$是一个与$e$相关的$(n,m)$译码函数。如果无论$x=e(b)$正确的传输或产生了$k$个或$k$个以下的错误并接收到的是$x_t$，都有$d(x_t)=b$，则称数据对$(e,b)$可以矫正$k$个或更少的错误。

下面开始介绍一种可以通过编码函数$e$得到相应的译码函数$d$的方法，被称为最大似然方法。

因为$B^m$有$2^m$个元素，所以$B^n$中也有$2^m$个元素与之对应，我们先把这$2^m$个元素按照某种次序排列。

$$
x^{(1)},x^{(2)},\cdots,x^{(2^m)}
$$

如果接收到的字是$x_t$，那么对于$1\leq i\leq 2^m$，计算$\delta (x^{(i)},x_t)$并且选取第一个代码字，譬如说$x^{(s)}$使得

$$
{\rm{min}}_{1\leq i\leq 2^m}\{\delta(x^{(i)},x_t)\}=\delta(x^{(s)},x_t)
$$

即：$x^{(s)}$是按照当前次序中第一个和$x_t$最接近的码字。

所以根据一开始排列顺序的不同，会得到不同的译码规则。

定理：假设$e$是一个$(m,n)$编码函数，$d$是与$e$相关的最大似然译码函数，那么$(e,d)$能纠正$k$个或更少的错误，当且仅当$e$的距离至少是$2k+1$。

定理：如果$K$是群$G$的一个有限子群，那么$G$中$K$每一个左陪集与$K$恰好有同样多的元素。

下面开始关注$e$是一个$(m,n)$编码函数，且是一个群码的情况，设它的代码字集合$N$是$B^n$的一个子群，$N=\{x^{(1)},x^{(2)},\cdots,x^{(2^m)}\}$。
假设代码字$x=e(b)$接收到的字是$x_t$。$N$由$x_t$确定的左陪集是：
$$
x_t\oplus N=\{\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_{2^m}\}
$$
从代码字$x_t$到$x^{(i)}$的距离恰好就是$|\varepsilon_i|$，因此若$\varepsilon_j$是有最小权的陪集成员，那么$x^{(j)}$一定是距离$x_t$最近的码字。在这种情况下$x^{(j)}=x_t\oplus \varepsilon_j$。一个有最小权的陪集元素$\varepsilon_j$被称为陪集首部。注意，由于排列次序的不同，一个陪集的首部不一定是唯一的。
如果$e:B^m\rightarrow B^n$是一个群码，那么下面就是得到$e$的最大似然译码函数的步骤：

1. 确定$B^n$中$N=e(B^m)$的所有左陪集。
2. 对于每个陪集求陪集首部。
3. 如果收到字$x_t$，那么确定$x_t$属于$N$的陪集。
4. 设$\varepsilon$是3.确定的陪集首部，计算$x_t\oplus \varepsilon$，那么$x_t$的译码就是$x_t\oplus \varepsilon$的译码。

由上述步骤1.2.确定的译码表如下所示：

译码表中每一行都是一个陪集，共有$2^r$个；每一行的第一个元素都是这个陪集的陪集首部。

在译码的时候只需要译$x_t$对应列首的元素即可。

至此，已经得出了译一般群码的通用方法。

下面介绍由特定的奇偶校验矩阵$H$确定的群码的译码方法。
由函数$f_H(x)=x*H$定义的函数$f_H:B^n\rightarrow B^r$是$B^n$到$B^r$的一个同态。
定理：由上述定义的函数同时是一个满射。
元素$x*H$称为$x$的校验子。
定理：设$x$和$y$是$B^n$中的元素，他们两个属于同一个左陪集的充分必要条件是$f_H(x)=f_H(y)$，即二者的校验子相同。
所以确定这种特殊的群码的译码函数的步骤如下：

1. 确定$B^n$中$N=e_H(B^m)$的所有左陪集。
2. 对于每个陪集，求出陪集首部和他的校验子。
3. 如果收到字$x_t$计算$x_t$的校验子，并且找到和$x_t$具有相同校验子的陪集首部$\varepsilon$，那么$x_t\oplus \varepsilon=x$是代码字$e_H(b)$，所以$d(x_t)=b$。

离散数学及其运用 第八章 高级计数基础

8.1 递推关系的应用

• 斐波那契数
• 汉诺塔问题
• 二进制串问题：给出一个长度为n且没有两个连续的0的二进制串的递推关系并给出初始条件

解：
长度为$n$且结尾是1的这样的二进制串，等于长度为$n-1$的这样的二进制串最后再加一个1。
长度为$n$且结尾是0的这样的二进制串，等于长度为$n-2$的这样的二进制串最后再加10。（可以仔细思考一下这之间的充分必要关系）
所以：$a_n=a_{n-1}+a_{n-2}$
其中$a_1=2$（0，1），$a_2=3$（01，10，11）

8.2 求解线性递推关系

• 定义1 一个常系数的$k$阶线性齐次递推关系是形如
  $$
  a_n=c_1a_{n-1}+c_2a_{n-2}+\cdots+c_ka_{n-k}
  $$
  的递推关系，其中$c_1,c_2,\cdots,c_k$是实数，$c_k\neq 0$

8.2.2 求解递推关系

求解递推关系就是直接把$a_n$显式的写成$a_n=f(n)$的形式，就算解出来了。

• 定理1 设$c_1$和$c_2$是实数。假设$r^2-c_1r-c_2=0$有两个不相等的根$r_1$和$r_2$，那么序列$\lbrace a_n\rbrace$是递推关系$a_n=c_1a_{n-1}+c_2a_{n-2}$的解，当且仅当$a_n=\alpha_1r_1^n+\alpha_2r^n_2$

  • 其中$\alpha_1$和$\alpha_2$是以下方程的解：
    $$
    a_0=\alpha_1+\alpha_2\\
    a_1=\alpha_1r_1+\alpha_2r_2
    $$

• 定理2 设$c_1$和$c_2$是实数。假设$r^2-c_1r-c_2=0$有两个相等的根$r_0$，那么序列$\lbrace a_n\rbrace$是递推关系$a_n=c_1a_{n-1}+c_2a_{n-2}$的解，当且仅当$a_n=\alpha_1r_0^n+\alpha_2nr^n_0$

• 定理3 设$c_1,c_2,\cdots,c_n$是实数。假设特征方程
  $$
  r^k-c_1r^{k-1}-\cdots-c_k=0
  $$
  有$k$个不相等的根$r_1,r_2,\cdots,r_k$。那么序列$\lbrace a_n\rbrace$是递推关系
  $$
  a_n=c_1a_{n-1}+c_2a_{n-2}+\cdots+c_ka_{n-k}
  $$
  的解，当且仅当
  $$
  a_n=\alpha_1r^n_1+\alpha_2r^n_2+\cdots+\alpha_kr^n_k
  $$

• 定理4 设$c_1,c_2,\cdots,c_n$是实数。假设特征方程
  $$
  r^k-c_1r^{k-1}-\cdots-c_k=0
  $$
  有$t$个不相等的根$r_1,r_2,\cdots,r_t$，其重数分别为$m_1,m_2,\cdots,m_t(m_1+m_2+\cdots+m_t=k)$。那么序列$\lbrace a_n\rbrace$是递推关系
  $$
  a_n=c_1a_{n-1}+c_2a_{n-2}+\cdots+c_ka_{n-k}
  $$
  的解，当且仅当
  $$
  a_n= (\alpha_1+\alpha_1n+\cdots+\alpha_{m_1-1}n^{m_1-1})r_1^n\\
  + (\alpha_2+\alpha_2n+\cdots+\alpha_{m_2-1}n^{m_2-1})r_2^n\\
  + \cdots+(\alpha_t+\alpha_tn+\cdots+\alpha_{m_t-1}n^{m_t-1})r_t^n
  $$

8.2.3 求解常系数线性非齐次递推关系

• 定理5 如果$\lbrace a_n^{(p)}\rbrace$是常系数非齐次线性递推关系
  $$
  a_n=c_1a_{n-1}+c_2a_{n-2}+\cdots+c_ka_{n-k}+F(n)
  $$
  的一个特解，那么每个解都是$\lbrace a_n^{(p)}+a_n^{(h)}\rbrace$的形式，其中$\lbrace a_n^{(h)}\rbrace$是相伴的齐次递推关系
  $$
  a_n=c_1a_{n-1}+c_2a_{n-2}+\cdots+c_ka_{n-k}
  $$
  的一个解。
• 如果$F(n)$是一次多项式，那么对于$\lbrace a_n^{(p)}\rbrace$的一个合理尝试是：$\lbrace a_n^{(p)}\rbrace=cn+d$。
• 如果$F(n)$是一个形如$q^n$（其中q为常数）的式子，那么对于$\lbrace a_n^{(p)}\rbrace$的一个合理尝试是：$\lbrace a_n^{(p)}\rbrace=C\cdot q^n$。

8.3 分治算法和递推关系

不考

8.4 生成函数

• 定义1 实数序列$a_0,a_1,\cdots,a_k,\cdots$的生成函数是无穷级数
  $$
  G(x)=a_0+a_1x+\cdots+a_kx^k+\cdots=\sum_{k=0}^\infty a_kx^k
  $$
• 二项式系数当上面的数是负数时
  $$
  \binom{-n}{r}=(-1)^rC(n+r-1, r)
  $$
  书上有一张表，叫做《有用的生成函数》，其实也不用看，记住泰勒公式就行了（虽然👴🏻也没记住，👴🏻就确实是废物）。

第10章 图

10.1 图和图模型

• 👴🏻找不到英文版书了，就先用这个凑活着，上考场看不懂就寄

👴🏻找到了

10.2 图的术语已经几种特殊的图

• 定理1 握手定理 设$G=(V,E)$是有$m$条边的无向图，则
  $$
  2m=\sum_{v\in V}deg(v)
  $$
• 定理2 无向图中有偶数个度为奇数的顶点。
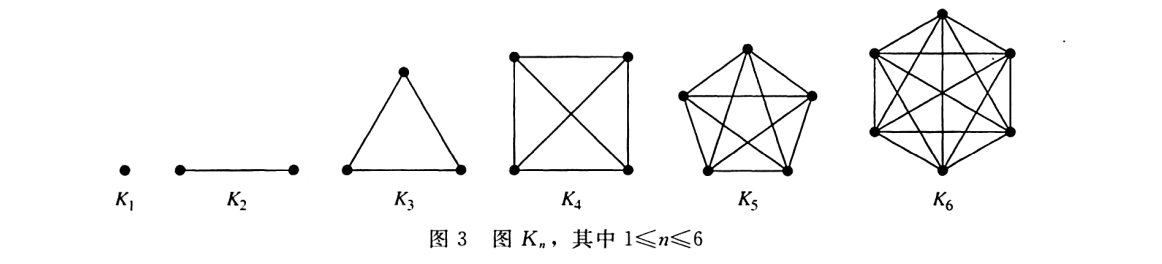
• 完全图$K_n$
  
• 圈图$C_n$
  
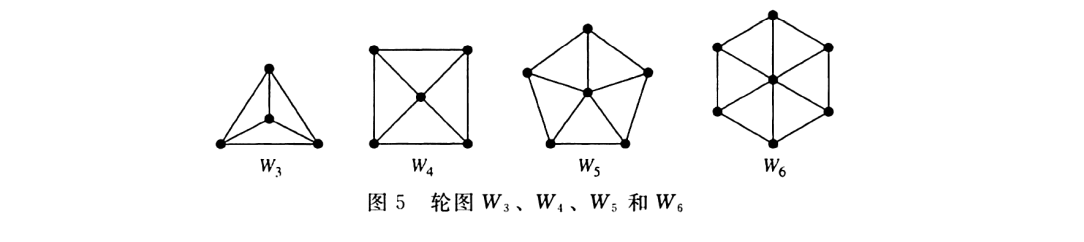
• 轮图$W_n$
  
• n立方体图$Q_n$
  
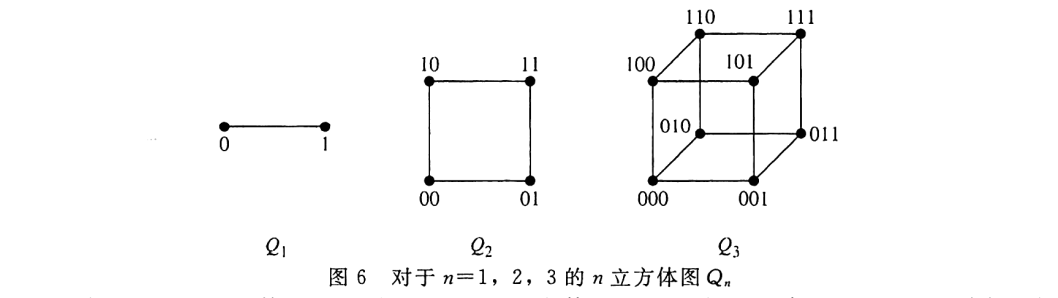
• 二分图，完全二分图$K_{m,n}$
  • 定理5 霍尔婚姻定理 带有二部划分$(V_1,V_2)$的二分图$G=(V,E)$中有一个从$V_1$到$V_2$的完全匹配，当且仅当对于$V_1$的所有子集$A$，有$|N(A)|\geq |A|$。
  • 看不懂就算了，先看别的最后回来再看这个

10.2 图的表示和图的同构

1. 图的邻接矩阵：行和列都是顶点
2. 图的关联矩阵：行是顶点，列是边

• 图的同构 $a$和$b$相邻当且仅当$f(a)$和$f(b)$相邻。
• 判断图的同构
  1. 先判断顶点数，边数，顶点的度是否相等
  2. 判断两个图的邻接矩阵，但邻接矩阵不同也不能说明两个图不同构，只能说明找的$f$不同构

判断图是否同构的充分必要条件尚未找到，只有这一堆必要条件和充分条件。若两个图满足很多的必要条件（也就是说他们看上去真的很像是同构的），但依然不是同构的，则称为魔鬼对。这个名字就很有意思。

10.4 连通性

1. 无向图的连通性
   定义3 若无向图中每一对顶点之间都有通路，则称该图是连通的。
2. 有向图的连通性
   定义4 若有向图中每一对顶点之间都有通路，则称该图是强连通的。
   定义5 若有向图所对应的无向图中每一对顶点之间都有通路，则称该图是弱连通的。
3. 有向图的强连通分支
   有向图$G$的子图是强连通的，但又不包含在任何其他更大的$G$的强连通子图中，则可称为$G$的强连通分支。

两个图同时存在长度为$k$的通路是两个图同构的必要条件

10.5 欧拉通路和哈密顿通路

1. 欧拉通路
   • 定理1 含有至少两个顶点的连通多重图具有欧拉回路的充分必要条件是每个顶点的度都为偶数。
   • 定理2 含有至少两个顶点的连通多重图具有欧拉通路但不具有欧拉回路的充分必要条件是恰有两个顶点的度为奇数。
2. 哈密顿通路
   目前还没有找到关于哈密顿通路的充分必要条件，但是找到了很多充分条件，这些充分条件都是本着一个朴素的想法产生的：一个图的边越多，越容易有哈密顿回路。
   • 定理3 狄拉克定理 在一个有$n$个顶点的简单图中（$n\geq 3$），若每个顶点的度都大于$n/2$则该图有哈密顿回路
   • 定理4 欧尔定理 在一个有$n$个顶点的简单图中（$n\geq 3$），若每一对不相邻的顶点之间都有$deg(u)+deg(v)\geq n$，则该图有哈密顿回路。

10.6 最短通路

1. Dijkstra
2. 邻接矩阵（Floyd）算法

https://blog.csdn.net/qq_35644234/article/details/60870719

10.7 平面图

定理1 欧拉公式 一个有$e$条边，$v$个顶点的平面图，将整个平面划分成$e-v+2$个面。
定理2 一个图不是平面图当且仅当它包含一个$K_{3,3}$或$K_5$的同胚。

10.8 图着色

定理1 四色定理 平面图的着色数不超过4。

• 着色多项式 不会，等神教我 会了，看神的博客

最大流算法

看书，不理解也没关系，就生搬硬套。

感谢菌，飞，以及平时诸多向我提出问题让我意识到自己的错误的同学对此篇笔记做出的贡献。